Los sorteos por apellidos de la administración pública dan a algunos candidatos muchas más probabilidades que a otros

Son muchas las administraciones en España que realizan sorteos por apellidos entre los aplicantes cuando hay empates a la hora de adjudicar plazas en algún proceso. Ocurre, por ejemplo, a la hora de elegir los miembros de un tribunal que juzgue unas oposiciones porque no suele haber voluntarios suficientes. Pasa también para determinar qué niño entra a un determinado colegio si la puntuación entre varios pequeños es la misma.

El sistema es sencillo. Se coge a todos los candidatos a la/s plaza/s y se ordenan alfabéticamente a partir de sus apellidos. Por sorteo se elige una letra (o dos) que determinan el apellido de la lista a partir del cual, por orden, se empiezan a adjudicar las plazas disponibles hasta que se agoten. Parece justo, cada letra tiene las mismas opciones de salir que las demás. No lo es. Ni de lejos.

“Aunque la elección de la pareja de letras sea uniformemente aleatoria, la distribución de las primeras letras de los apellidos en la población no es homogénea y tampoco lo será en un grupo concreto de participantes”, explica Ramiro Martínez Pinilla, doctorando en Matemática Aplicada en la Universidad Politécnica de Catalunya (UPC).

“Esto hace que, dada una lista, si realizamos el sorteo, no todos tengan la misma posibilidad de obtener una plaza y el sorteo sea manifiestamente injusto”, añade el autor de un estudio pionero sobre este tipo de sorteos que por primera vez pone en cifras las diferentes probabilidades que tiene cada apellido de salir en un concurso en función de la letra por la que comience, publicado en la revista TEMat de divulgación de trabajos de estudiantes de matemáticas.

En resumen: “Antes de que se realice el sorteo ya se sabe que hay personas que tienen muchas menos opciones. Si tu apellido empieza por detrás de una letra común (la G es la más presente) es muy posible que no te toque”. Un Sancho, por ejemplo, siempre irá detrás de todos los Sánchez.

Simplificando un poco, porque el asunto es complejo y más si se incluye una segunda letra, los apellidos que comienzan por H, N, S y T son los más perjudicados en este tipo de sorteo porque son las letras consecutivas a los apellidos más comunes (o beneficiados, si la idea es que no te toque, como por ejemplo en los tribunales de oposiciones, donde los docentes suelen preferir no estar).

En el otro extremo y por la misma razón, los apellidos que empiecen por la letra A siempre son los que más opciones tienen de salir, ya que si en el sorteo aparecen las letras V, W, X, Y o Z (cuando se llega al final se da la vuelta otra vez) apenas habrá candidatos con esos apellidos.

Hasta siete veces más probabilidades

Martínez ha plantado varios casos teóricos a partir de toda la población española. Le pidió los datos de los apellidos al Instituto Nacional de Estadística y empezó a realizar simulaciones de diferentes tipos de sorteos, cambiando el número de candidatos y el número de plazas para observar cómo afecta a las probabilidades de cada apellido según varían las condiciones de la convocatoria.

“Si los apellidos se escogen al azar [como ocurriría en un concurso de este tipo], lo que más influye es la proporción de plazas y candidatos. Con el triple de solicitantes que de plazas ya empieza a haber apellidos con el doble de probabilidades que otros. Me parece mucho. Y si aumentas el número de solicitantes, la diferencia se incrementa”, expone sus hallazgos. Si se sube la proporción a siete aspirantes por plaza, hay apellidos con un 32% de posibilidades de salir y otros con un 7%, cinco veces menos.

Las razones de esto son fáciles de entender. Aunque en un sorteo cada letra tiene las mismas opciones de salir (1 entre 27), los apellidos no se distribuyen uniformemente por el abecedario. Resulta obvio que en la sociedad hay muchos más Martínez, García o Sánchez que Burgos, Pozo o Villasante. Esto se verá reflejado en un concurso y lo condicionará.

Observe los gráficos que ilustran este artículo. Son dos concursos teóricos en los que se quiere otorgar 10 plazas. En uno hay 20 solicitudes, en el otro 40. Ambos se hacen a partir de una elección aleatoria de apellidos. En el que tiene 20 aspirantes, cada candidato debería tener a priori un 50% de probabilidades de que le tocara. Pero no es así. El gráfico claramente señala que los apellidados con la A están por encima del 60%, mientras que los de la N o la S están más cerca del 40%.

Álvarez vs Huertas

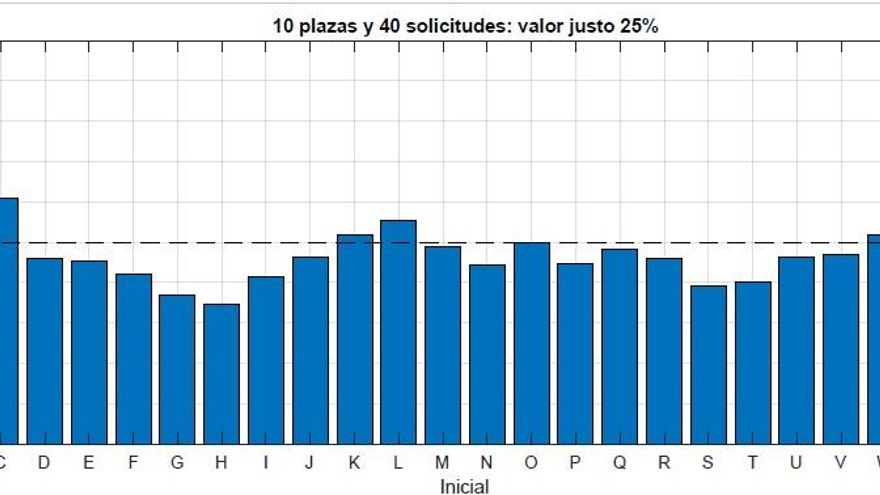
Aumentando el número de candidatos las diferencias aumentan, según señalaba Martínez. Se observa en el segundo gráfico, con 40 aspirantes y por tanto cada uno debería tener un 25% de opciones de salir. Sin embargo, de nuevo, los apellidados Álvarez o Zapatero rozarían el 40% de opciones, mientras que un Huertas apenas superaría el 15%, casi tres veces menos.

Cierto es que los sorteos se suelen hacer a partir de dos letras para dar más opciones (si fuera solo una, un Luengo siempre iría detrás de un López), pero esto no afecta tanto al resultado, explica Martínez: “La diferencia de hacerlo con una letra o dos solo es que hay un poco más de variabilidad”.

Este doctorando ha estudiado situaciones teóricas en todas las Comunidades Autónomas y ha llegado a la conclusión de que apenas hay diferencias entre ellas. La distribución de apellidos no varía tanto y lo importante, lo que afecta, siempre es la letra del apellido, cuenta.

La administración se desentiende

Martínez realizó el estudio movido por la curiosidad a partir de un proceso por este método en el que participó él para ingresar en una Escuela Oficial de Idiomas (EOI). Aunque en su caso sacó la plaza (y eso que la M no es de las mejores letras, según se ve en los gráficos), el concurso le abrió los ojos sobre la injusticia de estos métodos.

“En cuanto aprendí programación me puse por mi cuenta a ver las opciones de cada uno”, cuenta. Cuando acabó el estudio, se puso en contacto con el Procurador del Común de Castilla y León para explicarle por qué el método es injusto. “En su respuesta me dejó claro que ni entiende de Matemáticas ni siquiera había entendido la pregunta”, explica. “Me envió una carta con los apellidos más comunes en la comunidad”, se sorprende, “y diciéndome que como la ley dice que es así, pues es así. Es común, en todas las comunidades [que emplean este método] hay quejas todos los años que se archivan”.

También matiza el doctorando que “hay alguna excepción positiva en la que se ha dado la razón a quien planteaba los problemas”, y cita un ejemplo de 2004 en el que el defensor del pueblo aragonés dictaminó que deberían sustituirse estos sorteos por otros que dieran las mismas probabilidades a todos los candidatos.

En este momento, Asturias, Baleares, Canarias, Castilla y León, Extremadura, Galicia, Madrid (en el primer ciclo de Infantil, en el resto de etapas utilizan el método que se explica a continuación), Murcia, La Rioja y Valencia emplean este método.

¿Qué alternativa propone Martínez? Su propuesta es sencilla. Primero se ordenan los candidatos en una lista a partir de cualquier criterio (apellido, DNI, orden de inscripción...) y a cada uno se le asigna un número (el primero el 1, el segundo el 2, y así sucesivamente).

“Lo importante es que todas las posiciones tengan las mismas opciones de salir. Esto es lo que falla en los concursos en los que se extraen dos letras. Si no hay nadie cuyo apellido empiece por W, X, Y o Z, todas las parejas de letras que empiecen por ellas corresponderían a alguien apellidado Azaña, mientras que un Matute no podría tener ninguna papeleta si ya hay un Martínez”, explica.

Una vez ordenados y adjudicado un número a cada aspirante, se obtiene un número del 0 al 1 con decimales. Para ello se meten en un saco diez bolas numeradas del 0 al 9. Se extrae una al azar y ese será el primer decimal. Se mete la bola de nuevo en el saco y se extrae otra, el segundo decimal. Se pueden sacar tantos decimales como se quiera.

Si se hace ocho veces obtendremos un número entre 0,00000000 y 0,99999999 al que llamaremos r (pondremos de ejemplo que r=0,63807077). Se multiplica r por el número de aspirantes. Pongamos un caso teórico con 42 aspirantes. 42x0,63807077=26,79897234. Se empieza por el siguiente número, al que se le asigna la plaza. En este caso sería al candidato número 27. Luego a la 28 y así sucesivamente.

“El error de redondeo que se puede cometer decrece exponencialmente con el n´mero de decimales que tenga el número entre 0 y 1 que salga. Esta es la ventaja”, explica Martínez. “Una diferencia de 0,0000001 puntos porcentuales en la probabilidad de asignar la plaza puede ser asumible, una diferencia de 20 puntos porcentuales no lo es”, argumenta.

Este método ya lo utilizan algunas administraciones, cuenta Martínez. Para otras parece demasiado complejo de entender.